B⁺-tree

B⁺-tree는 키에 의해서 각각 식별되는 레코드의 효율적인 삽입, 검색, 삭제를 통해

정렬된 데이터를 표현하기 위한 트리자료구조입니다!

주로 데이터베이스에서 인덱스에 이용되고, 1장에서 배운 B-tree의 변형된 형태입니다!



B+ 트리는 인덱스구조에서 순차접근에 대한 문제의 해결책으로 제시되었습니다.

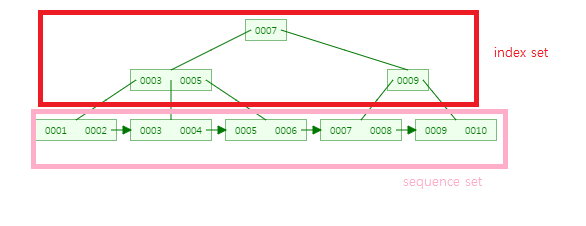
B-트리에서는 특정 key 값이 하나의 노드에서만 존재할 수 있지만, B+ 트리에서는 leaf 노드와 leaf의 부모 노드에서 공존할 수 있고,

B+ 트리의 비단말 노드(index set)들은 데이터의 빠른 접근을 위한 인덱스 역할만 하기 때문에 키와 포인터로만 구성되어있습니다.



그리고 leaf 노드들은 연결 리스트 형태로 서로 연결되어 있고 이를 순차집합(sequence set)이라고 하며 오름차순으로 정렬이 되어 있습니다.

고로 B+ 트리는 (기존의 B-트리 + 데이터의 연결 리스트)로 구현된 색인구조라고 할 수 있습니다.

이 때문에 순차적인 탐색에 매우 유리합니다~!

B-tree의 변형이므로 B-tree와 유사합니다!

차이점은 다음과 같습니다!

• B-tree의 각 노드에서는 key 뿐만 아니라 data도 들어 갈 수 있지만, B⁺-tree에서는 순차집합에만 데이터가 들어갈 수 있다.

• B⁺-tree는 B-tree와 달리 삽입, 삭제연산이 leaf에서만 이루어진다.

• B⁺-tree는 leaf node 끼리 연결리스트로 연결되어 있다.

B⁺-tree 삽입

B⁺-tree 삽입은 B-tree와 비슷하게 overflow되면 split됩니다!

다른 점은 순차 세트 부분에 키가 중복되어 존재하고, 연결리스트 형태로 연결되어 있다는 것입니다.

또, M이 홀수일 때, overflow가 되어 분할되서 부모로 올리는 값은 ┌M/2┐+1번째 값이라는 것입니다.

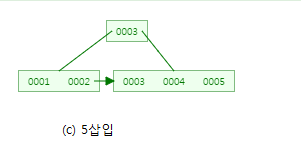
한 번 3차 B⁺-tree에 1부터 10까지 삽입해보겠습니다.



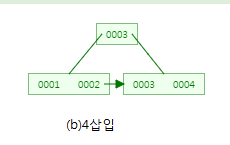
1부터 3까지는 overflow가 발생하지 않기에 그냥 삽입됩니다.

4 삽입시 overflow가 발생하기에 ┌3/2┐+1=3번째 값인 3을 부모노드로 올리고 좌우로 분할하고 데이터를 삽입합니다.

이 때 부모노드로 올리는 3는 리프노드(순차세트)에도 그대로 남게 됩니다.

또 리프노드끼리는 연결리스트 형태로 연결됩니다.

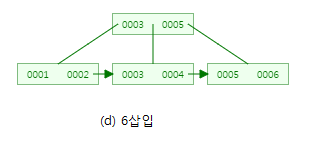
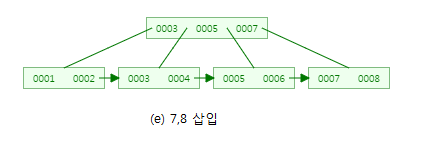
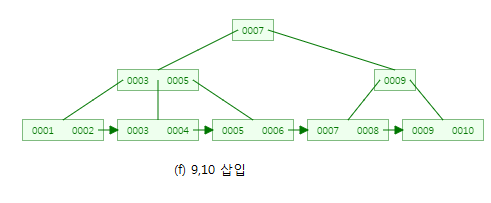
B-트리 삽입연산과 조금밖에 다르지 않죠?? 이어서 다른 값들도 삽입해보겠습니다.

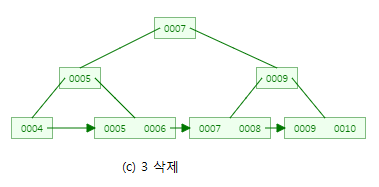
B⁺-tree 삭제

B-tree와 다르게 B⁺-tree의 삭제연산은 leaf node에서만 실행되기에 단순합니다.

• 키 값을 삭제했을 때 leaf node가 underflow 되지 않으면, 키값을 삭제하고 index set에서의 값도 삭제 후 적절한 key값을 그 자리에 넣는다.

• 키 값을 삭제했을 때 leaf node가 underflow 되면, 형제노드에게 값을 빌린거나 병합한다(B-tree 삭제와 유사)

한 번 삭제연산을 해보죠!

아까 1부터 10까지 삽입한 3차 B⁺-tree를 그대로 이용하겠습니다.

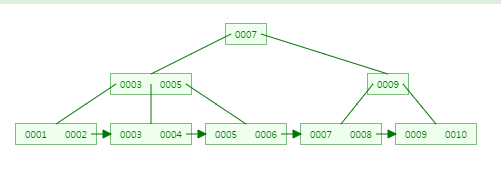
먼저, 2를 삭제하겠습니다!

2를 삭제해도 leaf node에서 underflow가 발생하지 않으므로, 2를 그냥 삭제합니다.

index set엔 2가 없으므로 변경할 필요가 없습니다!

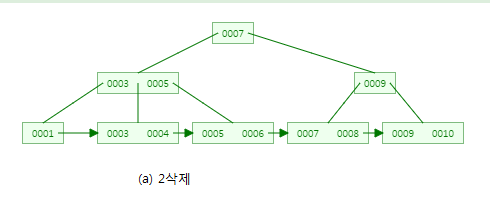
이 때 1을 삭제하겠습니다!

그러면 leaf node에서 underflow가 발생하게되고, 형제노드 (3,4)를 확인합니다.

값을 빌릴 수 있는 여건이 되기에 3을 1이 있던 노드에 빌려줍니다.

어떻게 보면 형제노드(3,4)에서는 3이 삭제된 것과 같으므로 index node에 있는 3을 삭제하고, 4로 대체해줍니다!

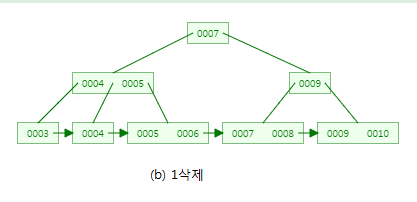
마지막으로 3을 삭제하겠습니다.

3을 삭제하면, leaf node에서 underflow가 발생하게되고, 형제노드 (4)를 확인합니다.

값을 빌릴 수 있는 여건이 되지 않으므로 형제노드(4)와 부모노드(4)와 병합합니다.