[자료구조] 1.B-tree
in Study on DataStructure
검색을 위한 이진탐색트리
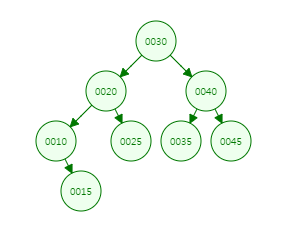
이진탐색트리는 컴퓨터 트리 자료구조로 각각의 노드가 최대 두 개의 자식 노드를 가집니다.
부모노드를 기준으로 왼쪽서브트리의 노드들은 모두 부모노드보다 작고, 오른쪽 서브 트리의 노드들은 모두 부모노드보다 큽니다.
이러한 특성 덕분에 어떤 수를 탐색할 때 시간복잡도는 트리의 높이가 h라고 했을 때, O(h)가 됩니다.
만약 n개의 노드를 가지는 이진트리가 완전 이진 트리처럼 균형이 잡혀있다면 높이가 ┌log2n ┐ 이므로, 시간복잡도가 O(┌log2n ┐)가 됩니다!
하지만, 이진탐색 트리가 다음과 같이 경사 이진 트리 형태이면, 높이가 n이므로 0(n)의 시간복잡도를 가져서 비효율적입니다.
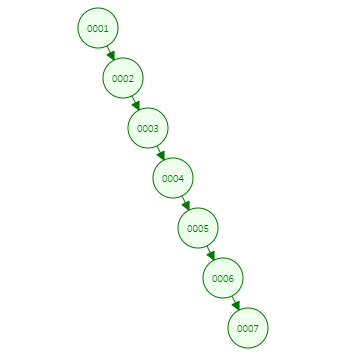
이러한 문제점을 해결하기 위해 Balance tree가 등장했습니다.
Balance tree는 노드가 삽입될 때마다 자동으로 균형을 맞춰주는 트리입니다.
B-tree와 B+-tree, B*-tree 는 Balance tree 중 하나로 이진 트리와 다르게 노드가 2개이상의 자식을 가질 수 있습니다.
주로 데이터베이스의 인덱스가 B-tree 구조입니다.
한 번 살펴보죠!
B-tree
M차 b-tree는 한 노드에 들어갈 수 있는 최대 키의 개수가 M개입니다.
M차 B-tree의 특성은 다음과 같습니다.
1.한 노드의 키가 N개라면, 그 노드의 자식의 갯수는 반드시 N+1이어야 한다.(따라서 tree의 max degree는 M+1)
2.root node가 leaf node 인 경우를 제외하고 항상 최소 2개의 자식을 가진다.
3.root node를 제외한 모든 노드는 적어도 ┖M/2┙개의 키를 가지고 있어야한다.
4.모든 leaf node 들은 같은 level에 있어야 한다.
5.node 내의 key 값들은 오름차순이다.(중복된 키 허용x)
6.node의 자료 Dk 왼쪽 서브트리는 Dk보다 작은 값들이고, 오른쪽 서브트리는 Dk보다 큰 값들이다.
아 그리고 M(차수)가 짝수냐 홀수냐에 따라서 알고리즘이 다릅니다!
저는 M이 홀수인 경우라고 가정하고, 포스팅하겠습니다!
B-트리 삽입
삽입 규칙은 다음과 같습니다. (홀수 차수 B-tree)
- 자료는 항상 leaf 노드에 추가된다.
- 추가될 leaf노드에 여유가 있다면 그냥 삽입
- 추가될 leaf노드에 여유가 없다면 ┌M/2┐번째 키값을 부모노드로 옮기고 좌우로 분할 후 삽입
한 번 직접 실습해볼까요??
다음 사이트는 B-트리를 그릴 수 있는 사이트입니다
https://www.cs.usfca.edu/~galles/visualization/BTree.html
3차 B-트리에 1부터 10까지 삽입해 보겠습니다. (tree의 degree는 4)
그러면 각 노드는 최대 3개의 키 값을 가질 수 있습니다~!
따라서 1부터 3까지 삽입은 다음과 같이 하나의 노드에 삽입됩니다.

그 다음 4를 삽입하면 노드가 가질 수 있는 최대 키의 개수를 넘기에 ┌3/2┐=2번째 값인 2를 부모노드로 올립니다.
그리고 2를 기준으로 분기 후 4를 삽입합니다.
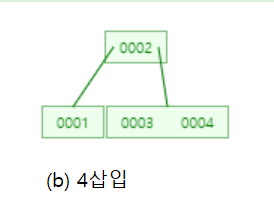
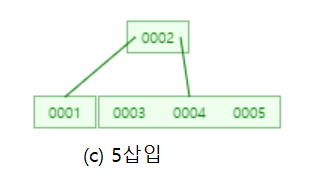
6을 삽입할 때 또 노드가 가질 수 있는 키의 값을 넘으므로 ┌3/2┐=2번째 값인 4를 부모노드로 올리고,
양쪽으로 분기한 후 삽입합니다!
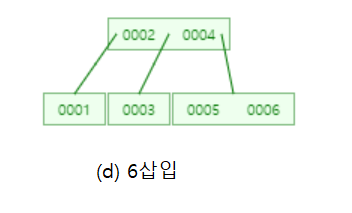
어때요?? 생각보다 쉽죠! 나머지 수도 삽입해보겠습니다.
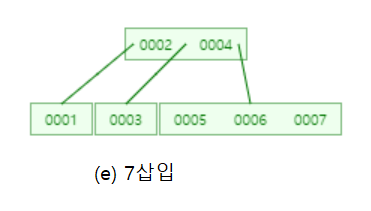
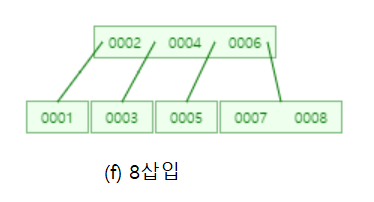
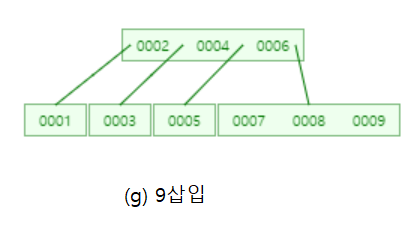
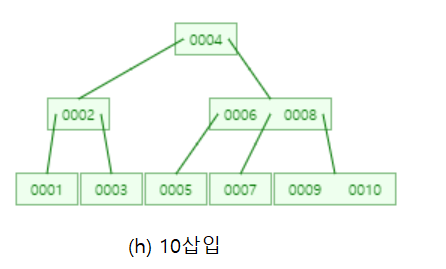
어때요~ 이진탐색트리에서 1부터 10까지 삽입하면 경사이진트리가 되는데 B-트리는 자동으로 균형을 맞추었죠??
이것이 B-트리의 장점입니다!
B-트리 삭제
먼저, 삭제하고자 하는 자료가 있는 노드가 삭제후 자료수가 ┖M/2┙이상이 되도록 보장해야함을 명심해야합니다.
B-트리의 삭제규칙은 다음과 같습니다. (홀수차수 B-트리)
CASE-1: 삭제하는 키 값이 존재하는 node가 leaf node인 경우
- (a) 키를 삭제 후에도 node의 자료수가 ┖M/2┙이상이면 그냥 키를 삭제한다.
- (b) 키를 삭제 한 후에 node의 자료수가 ┖M/2┙가 안 되면, 형제 node에서 빌린다.
- (c) 키를 삭제 한 후에 node의 자료수가 ┖M/2┙가 안 되고, 형제 node에서 빌릴 수 없으면 형제 노드와 합병한다.
CASE-2: 삭제하는 키 값이 존재하는 node가 internal node인 경우
- (a)대체키를 찾아야하는데, 왼쪽 서브트리의 가장 큰 값 또는 오른쪽 서브트리의 가장 작은 값으로 대체한다.
- (b)대체키로 키 값을 바꾸는 과정에서 case 1을 이용해 적절히 처리해준다.
예를 들어 다음과 같은 5차 B-tree가 있다고 합시다!
그러면 root node를 제외한 node는 최소 ┖M/2┙=2개 이상의 키를 가져야합니다!
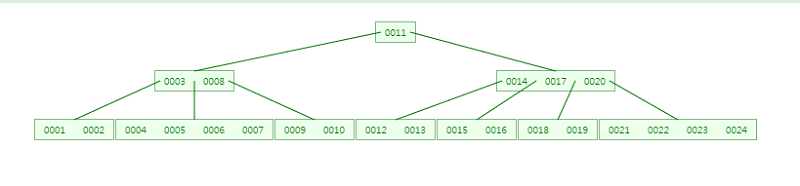
CASE:1-(a) 4를 삭제
해당 노드의 키값은 2개 이상이므로 그냥 4를 삭제하면 됩니다.
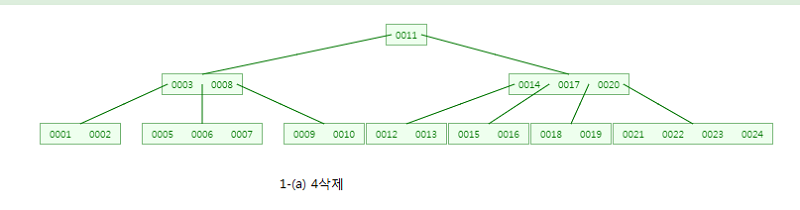
CASE:1-(b) 1을 삭제
1을 삭제하면 해당 노드의 자료수가 1개이므로 최소 2개이상의 자료를 가져야한다는 조건을 위배합니다.
이 때 형제노드(5,6,7)를 살펴봅니다~
형제 노드(5,6,7)의 자료를 한 개 삭제했을 때에도 형제 노드의 자료수가 2개이상이므로
가장 작은 값 5를 부모노드로 올리고,
부모노드의 3을 1이 삭제된 노드로 옮깁니다!
즉, 형제 노드에게 키를 빌립니다!
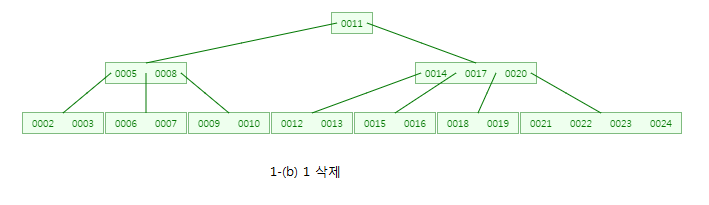
형제 노드에게 값을 직접 빌리는 건 아니지만 표현을 그렇게 한것입니다!
그리고 만약 좌측 형제노드에게 값을 빌릴 때는 형제 노드의 가장 큰 값을 부모노드로 올립니다!
CASE:1-(c) 13를 삭제
13를 삭제하면 해당 노드의 자료수가 1개이므로 최소 2개이상의 자료를 가져야한다는 조건에 위배됩니다.
이 때 형제노드 (15,16)을 살펴 봅니다.
그런데 형제노드도 값을 빌려줄 여건이 되지 않습니다!(최소 2개이상의 자료를 가져야하므로)
이럴 때는 부모노드의 값(14)를 내려서 원래노드와 부모노드와 형제노드를 병합합니다!
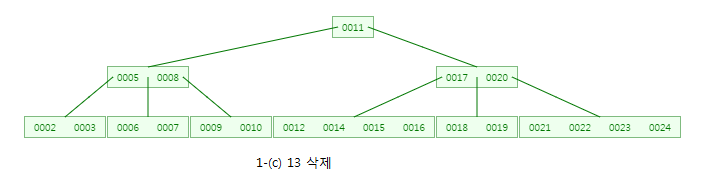
이번에는 내부노드가 삭제되는 과정을 살펴보겠습니다!
5차 B-tree가 다음과 같이 있다고 합시다!
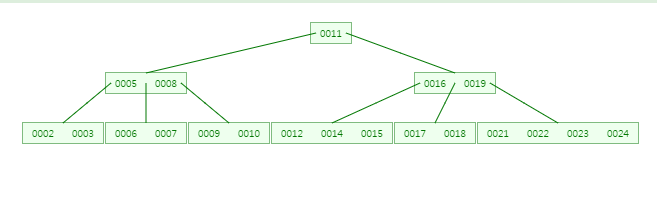
CASE:2-(a) 16 을 삭제
16이 있는 노드는 내부 노드이므로 대체할 값이 필요합니다.
이 때 왼쪽 서브트리의 가장 큰 값 15로 대체합니다~!
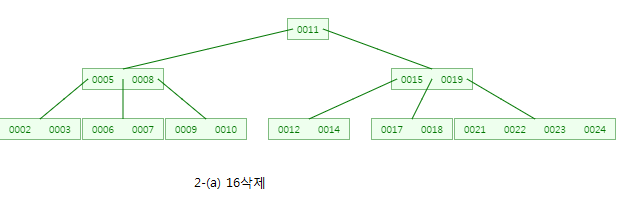
CASE:2-(b) 19를 삭제
19를 포함한 노드도 내부노드이므로 19를 삭제하면 좌측 서브트리의 가장 큰 값인 18로 대체합니다~
하지만 18을 포함한 노드의 자료수가 2개이상이 아니므로,
CASE 1-(b)에 의해 형제노드 (21,22,23,24)에서 21을 부모노드로 올리고, 18을 다시 내립니다!
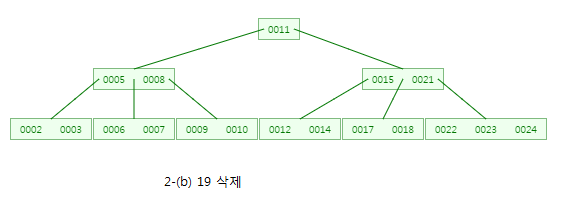
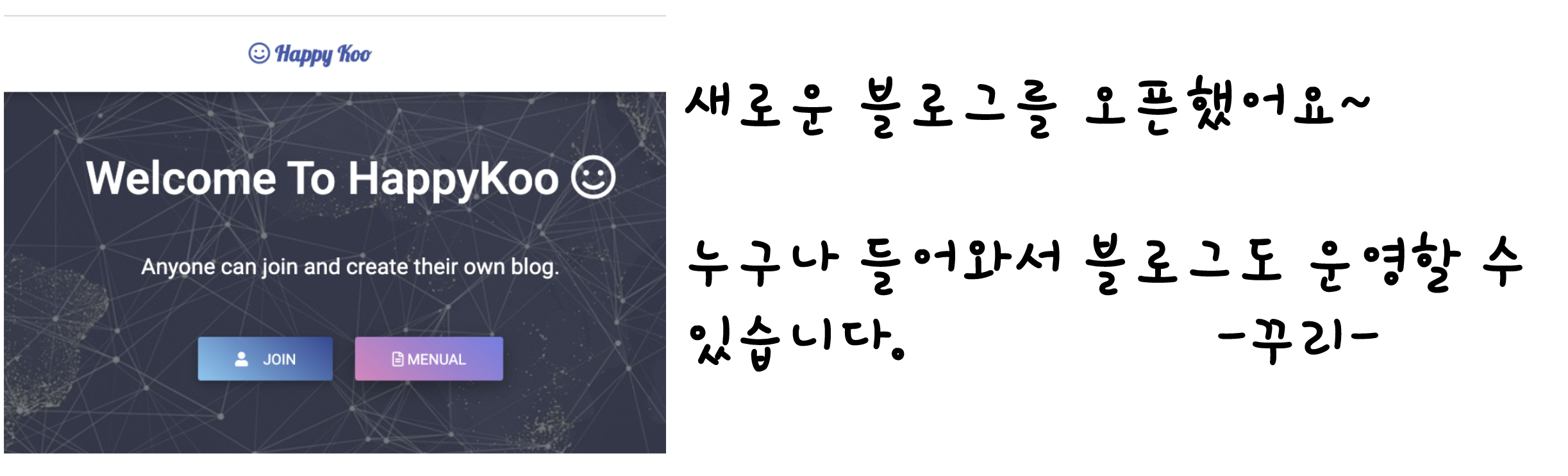
CASE:2-(b) 11를 삭제
11을 포함한 노드는 내부노드이므로 대체할 키를 찾아야합니다.
좌측 서브트리의 가장 큰 값인 10을 먼저 대체합니다~!
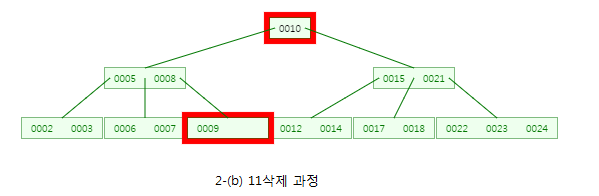
하지만 원래 10를 포함한 내부노드가 자료수가 1개가 되므로 형제노드(6,7)을 살펴봅니다~
형제노드도 값을 빌려줄 여건이 안되므로 CASE1-(c)에 의해 부모노드(8)과 형제노드(6,7)와 병합합니다.
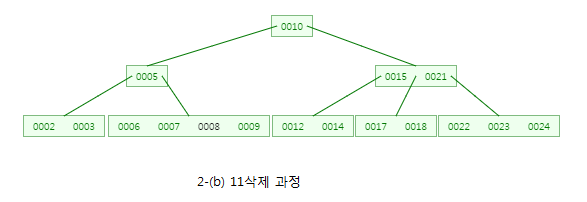
그러면 이제 원래 8을 포함한 노드의 자료수가 1개가 됩니다.
이 때 형제노드(15,21)에게 값을 빌릴 수 있는지 확인하지만, 빌릴 수 없네요~
따라서 부모노드(10)과 형제노드(15,21)과 병합합니다.