[matlab] 14.미분방정식의수치해법(2)

in Language on matlab


경계값 문제



전 장에서는 미분방정식에서 초기값이 주어졌을 때의 해결방법을 알아봤었는데요~

이번 시간에는 경계값이 주어졌을 때의 미분방정식의 해결방법을 확인해보겠습니다.

2계 이상의 미분방정식에 관한 문제 중에는 종속변수 y 또는 이것의 도함수들의 서로 다른 점에서의 값이 주어졌을 때 해를 구하는 문제가 있습니다.

이와 같이 주어진 미분방정식과 경계에서의 조건을 만족하는 해를 구하는 문제를 경계값 문제라 하고,

아래와 같은 형태의를 경계값 문제라고 합니다.


image



선형 shooting 방법



일반적으로 경계값 문제는 초기값 문제보다 수치해를 구하기가 어렵습니다.

그래서 경계값 문제를 초기값 문제로 대체하여 풀 수 있는데,

아래의 방식은 선형 shooting 방법에 대한 설명입니다!


image



초기값 문제는 앞서 배운 Euler 방법이나 Runge-Kutta 방법을 사용해서 풀 수 있습니다~!

Euler 방법을 사용하여 Shooting 방법의 한 부분인 반복법을 나타내면 다음과 같습니다.


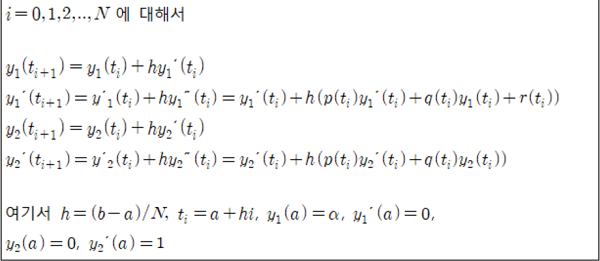
image




image



자 그러면, 예제를 풀어보면서 선형 shooting 방법을 익혀보겠습니다.


image



matlab 코드입니다. 


%%%%%%%shooting 방법%%%%%%%%%
%p(x)=1 q(x)=1
clear; clc; clf; n=20;
x=linspace(0,pi,n+1); h=x(2)-x(1);
ex=x.*cos(x)+sin(x); %%정확한 해
alpha=0; beta=-pi;
rx=@(x)-2*(1+x)*cos(x)+(x-4)*sin(x); %r(x)
u1(1)=alpha; %y1(0)=0(alpha)
v1(1)=0; %y1'(0)=0
u2(1)=0; %y2(0)=0
v2(1)=1; %y2'(0)=1

for i=1:n
    u1(i+1)=u1(i)+h*v1(i);
    v1(i+1)=v1(i)+h*(v1(i)+u1(i)+rx(x(i)));
    u2(i+1)=u2(i)+h*v2(i);
    v2(i+1)=v2(i)+h*(v2(i)+u2(i));
end
y=u1+u2*(beta-u1(end))/u2(end);
plot(x,y,'ko',x,ex,'k-')
legend('shooting 방법','정확한 해')



실행결과입니다~


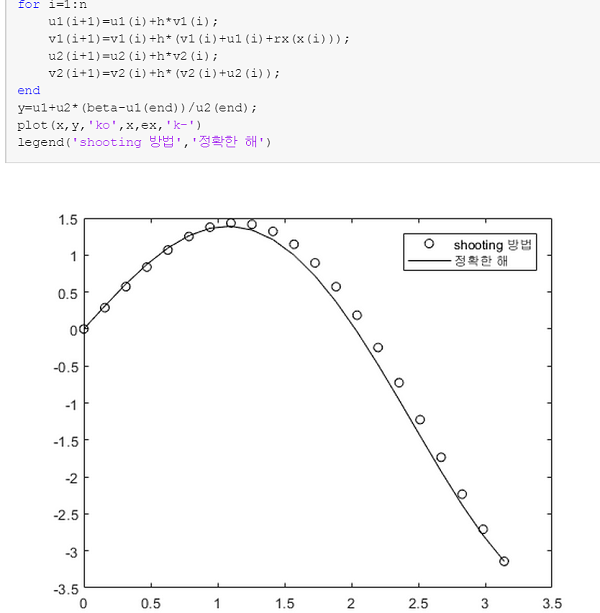
image



수치해가 잘 구해지는 것을 보실 수 있습니다~

Runge-Kutta 방법으로도 가능합니다. 


clc; clear; clf;
n=100; beta=-pi;
t=linspace(0,pi,n);
h=t(2)-t(1);
r=@(t)-2*(1+t)*cos(t)+(t-4)*sin(t);
f1=@(t,X)X(1)+X(2)+r(t);
f2=@(t,X)X(1)+X(2);
g=@(t,X)X(1);
F1=@(t,X)[f1(t,X),g(t,X)];
F2=@(t,X)[f2(t,X),g(t,X)];
x0=[0 0];
x1=[1 0];
u1=runge_kutta(F1,t,x0);
u2=runge_kutta(F2,t,x1);
u1=u1(:,2);
u2=u2(:,2);
y=u1+u2*((beta-u1(end))/u2(end));
plot(t,y,'ko',t,t.*cos(t)+sin(t),'r-')



비 선형 shooting 방법



이제는 2계 경계값 문제 중 방정식이 비선형인 경우에 대해 알아보도록 하겠습니다.

비선형 2계 경계값 문제는 비선형 문제의 해가 두개의 초기값 문제의 해의 일차결합으로 표현할 수 없다는 점을 제외하고,

선형 shooting방법과 비슷하게 풀 수 있습니다.

비선형 shooting 방법에 대해 알아보죠!


image




image



많이 어려우시죠?? 예제를 풀어보면서 익혀나가봅시다!


image



matlab 코드입니다~ 


%%%%%%%shooting 방법%%%%%%%%%
clear; clc; clf;
epsilon=0.5; n=20; flag=1; k=1;
alpha=0; beta=tanh(1/(sqrt(2)*epsilon));
x=linspace(0,1,n+1); h=x(2)-x(1); 
ex=tanh(x/(sqrt(2)*epsilon)); %정확한해
tol=1.0e-5; %오차 
t(k)=(beta-alpha/(1-0)); %%t(0)=(beta-alpha)/(b-a)
y(1)=0; %y(0,t(k))=alpha
z(1)=0; %z(0,t(k))=0
dz(1)=1; %z'(0,t(k))=1
plot(x,ex,'k-')
hold on
while flag==1
    dy(1)=t(k); %y'(0,t(k))=t(k)
    for i=1:n
        y(i+1)=y(i)+h*dy(i);
        dy(i+1)=dy(i)+h*(y(i)^3-y(i))/epsilon^2;
        z(i+1)=z(i)+h*dz(i);
        dz(i+1)=dz(i)+h*(3*y(i)^2-1)*z(i)/epsilon^2;
    end
    if abs(y(end)-beta)<tol||k>2 %y(N,t(k))-beta가 tol보다 작거나 3번 shooting을 반복하면 빠져나옴
        flag=0;
    end
    k=k+1; t(k)=t(k-1)-(y(end)-beta)/z(end);
    if k==2 %2번째 반복일 때의 그래프
        plot(x,y,'ko')
    elseif k==3 %3번째 반복일 때의 그래프
        plot(x,y,'kd')
    else %1번째 반복일 때의 그래프
        plot(x,y,'ks')
    end
end
hold off
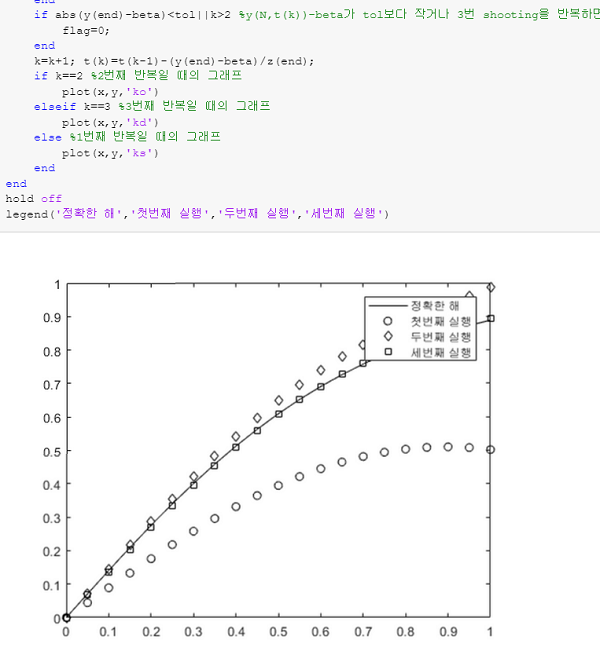
legend('정확한 해','첫번째 실행','두번째 실행','세번째 실행')



실행결과입니다


image