[matlab] 13.미분방정식의수치해법(1)

in Language on matlab


미분방정식의 수치해법 - 초기 값 문제



이번 장에서는 미분방정식의 수치해법 중 초기값을 이용한 벙법 중 Euler, 향상된 Euler, 중간점방법,

Runge-Kutta 방법에 대해 알아보고, 이를 이용하여 연립방정식의 해를 찾아볼 것입니다~!



Euler 방법



먼저, Euler방법에 대해 알아보겠습니다.


image



예제를 matlab으로 풀어보면서 Euler 방법을 익히도록 하겠습니다!


image



matlab으로 해를 구해보고, 과연 정확한 해와 비교하여 얼마나 정확한지 그림으로 확인해보겠습니다.

matlab 코드입니다! 


%%%%%%%%%%Euler%%%%%%%%%%%
clear; clf; clc;
h=0.01; %단계크기
t0=0; T=1; %처음 점과 끝 점
t=t0:h:T;
N=length(t);
y(1)=2; %초기 값
f=@(ft,fy)1-2*ft+5*fy; % 함수 정의
for i=1:N-1
    y(i+1)=y(i)+h*f(t(i),y(i)); %오일러 방법
end

exy=53/25*exp(5*t)+2/5*t-3/25; %정확한 해

%구한 해와 정확한 해 비교
plot(t,y,'ko',t,exy,'k')
legend('오일러 방법','정확한 해')



실행결과입니다~


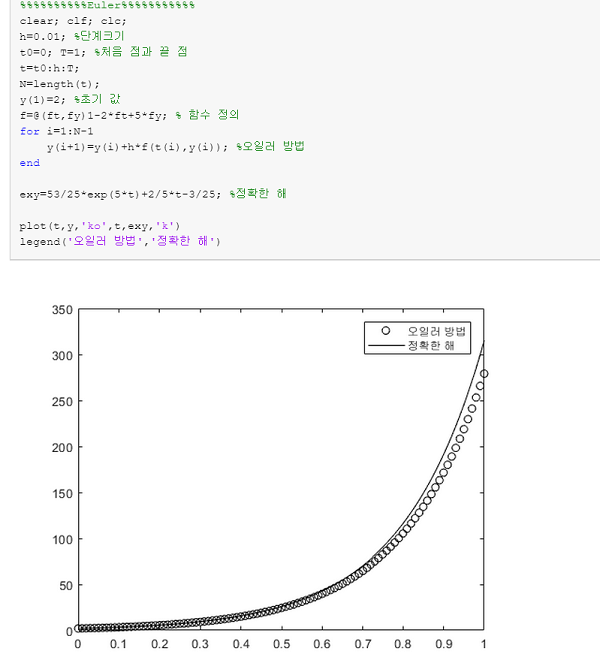
image



상당히 비슷한 것을 볼 수 있습니다~!



수정 된 Euler 방법과 중간점 방법



이번에는 Euler 방법보다 더 정확한 방법에 대해 알아보겠습니다.

바로 수정된 Euler 방법과 중간점 방법입니다~

증명은 생략하고~~ 식만 살펴본 후에 matlab을 통해 얼마나 정확한 지에 대해 살펴보겠습니다.


image



저 식을 예전에 Euler 방법에서 사용한 식 대신에 이용만 하면 됩니다!

간단하죠??

한 번 아까 예제를 matlab으로 구현해보겠습니다! 


%%%%%%%%%%수정된 Euler%%%%%%%%%%%
clear; clf; clc;
h=0.01; %단계크기
t0=0; T=1; %처음 점과 끝 점
t=t0:h:T;
N=length(t);
y(1)=2; %초기 값
f=@(ft,fy)1-2*ft+5*fy; % 함수 정의
for i=1:N-1
    y(i+1)=y(i)+(h/2)*(f(t(i),y(i))+f(t(i+1),y(i)+h*f(t(i),y(i)))); %수정된 오일러 방법
end

exy=53/25*exp(5*t)+2/5*t-3/25; %정확한 해

plot(t,y,'ko',t,exy,'k')
legend('수정 된 오일러 방법','정확한 해')

실행결과입니다~


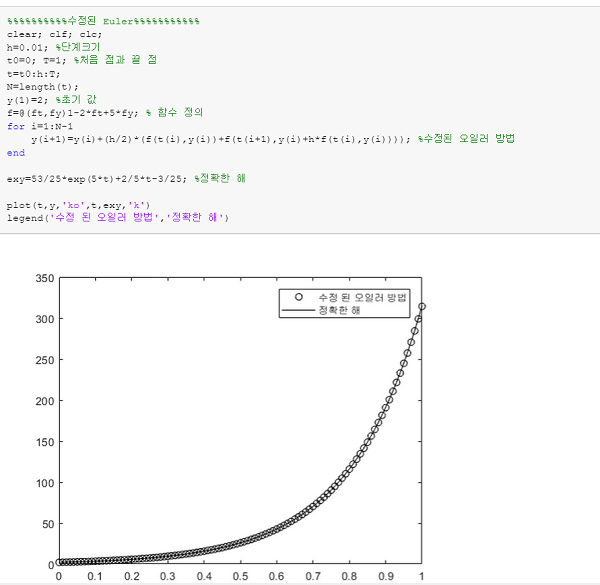
image



정확한 해와 거의 같은 것을 볼 수 있습니다~

이번에는 중간점 방법을 이용한 matlab 코드입니다~ 


%%%%%%%%%%중간점 방법%%%%%%%%%%%
clear; clf; clc;
h=0.01; %단계크기
t0=0; T=1; %처음 점과 끝 점
t=t0:h:T;
N=length(t);
y(1)=2; %초기 값
f=@(ft,fy)1-2*ft+5*fy; % 함수 정의
for i=1:N-1
    y(i+1)=y(i)+h*f(t(i)+1/2*h,y(i)+1/2*h*f(t(i),y(i))); %중간점 방법
end

exy=53/25*exp(5*t)+2/5*t-3/25; %정확한 해

plot(t,y,'ko',t,exy,'k')
legend('중간점 방법','정확한 해')



실행결과입니다~!


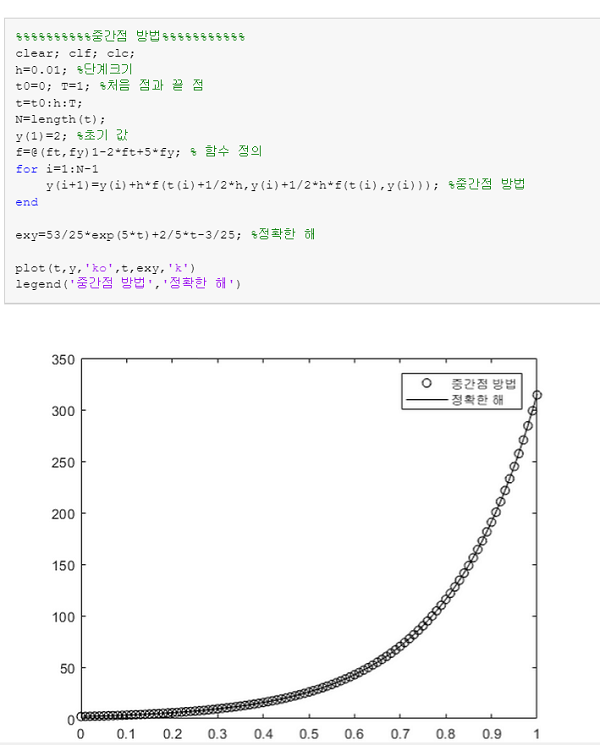
image



역시 해를 잘 찾아내는군요!!



Runge-Kutta 방법



마지막으로, 지금까지의 방법보다 더 정확한 4차 Runge-Kutta(RK4)방법에 대해 살펴보겠습니다.

Runge-Kutta 방법으 테일러 방법을 개선한 방법으로 높은 차수의 오차 한계는 그대로 유지하면서,

고차의 도함수를 구할 필요성을 없앤 방법입니다.

식만 한 번 살펴볼까요??


image



굉장히 복잡해보이지만, 저식 그대로 이전의 식에 옮기면 됩니다!

한 번 matlab으로 구현해보겠습니다. 


%%%%%%%%%%Runge-Kutta 방법%%%%%%%%%%%
clear; clf; clc;
h=0.01; %단계크기
t0=0; T=1; %처음 점과 끝 점
t=t0:h:T;
N=length(t);
y(1)=2; %초기 값
f=@(ft,fy)1-2*ft+5*fy; % 함수 정의
for i=1:N-1
     k1=h*f(t(i),y(i)); %Runge-Kutta 방법
     k2=h*f(t(i)+h/2,y(i)+1/2*k1);
     k3=h*f(t(i)+h/2,y(i)+1/2*k2);
     k4=h*f(t(i+1),y(i)+k3);
     y(i+1)=y(i)+1/6*(k1+2*k2+2*k3+k4);
end

exy=53/25*exp(5*t)+2/5*t-3/25; %정확한 해

plot(t,y,'ko',t,exy,'k')
legend('Runge-Kutta 방법','정확한 해')



실행결과입니다~!


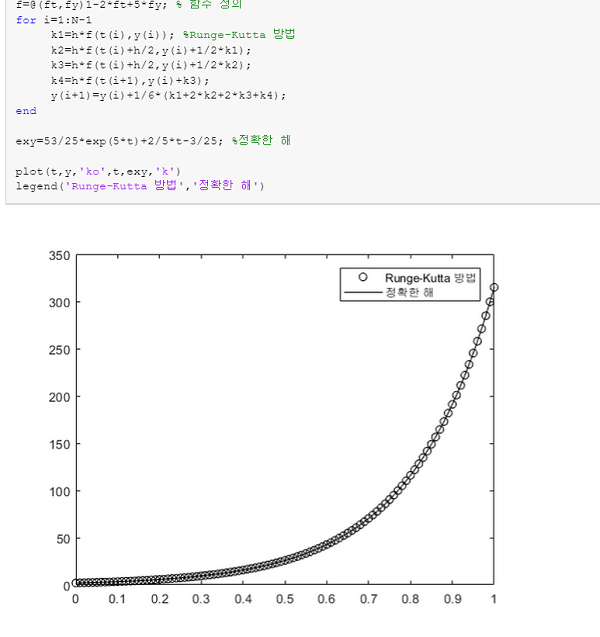
image



Euler방법보다 훨씬 더 정확한 방법이니 잘 알아두시길 바랍니다~!

지금까지 초기 값이 주어진 일차 미분방정식을 푸는 해법에 대해 알아봤습니다.

그렇다면 연립 미분방정식은 어떻게 풀까요? 위의 방법을 그대로 이용하게 됩니다!



연립 일차 미분방정식



초기값이 주어진 연립 일차 미분방정식을 푸는 방법에 대해 살펴보도록 하겠습니다.


image



그저 벡터화 시킨다음에 아까 배웠던 방법을 쓰면 됩니다! 참 쉽죠??(농담입니다)

예제를 matlab으로 풀어보면서 이번 장을 마무리 하겠습니다!


image



matlab 코드입니다!

어떤 연립 미분방정식도 풀 수 있도록 Runge-Kutta 함수를 먼저 정의하겠습니다. 


function y=runge_kutta(f,t,x0)
h=t(2)-t(1); %점과 점사이의 거리
M=length(x0); %방정식의 개수
N=length(t);
y=zeros(N,M); %연립미분방정식의 해
y(1,:)=x0; %초기값 저장
for i=1:N-1 %Runge_Kutta 방법(벡터이기에 인덱스를 조심해야한다)
    K1=h*f(t(i),y(i,:)); 
    K2=h*f(t(i)+h/2,y(i,:)+1/2*K1);
    K3=h*f(t(i)+h/2,y(i,:)+1/2*K2);
    K4=h*f(t(i+1),y(i,:)+K3);
    y(i+1,:)=y(i,:)+1/6*(K1+2*K2+2*K3+K4);
end



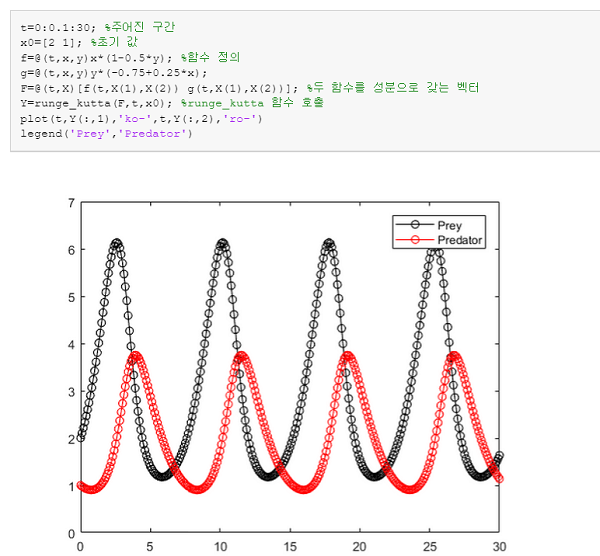
이를 이용해서 포식자 문제를 풀어보죠! 


t=0:0.1:30; %주어진 구간
x0=[2 1]; %초기 값
f=@(t,x,y)x*(1-0.5*y); %함수 정의
g=@(t,x,y)y*(-0.75+0.25*x);
F=@(t,X)[f(t,X(1),X(2)) g(t,X(1),X(2))]; %두 함수를 성분으로 갖는 벡터
Y=runge_kutta(F,t,x0); %runge_kutta 함수 호출
plot(t,Y(:,1),'ko-',t,Y(:,2),'ro-') 
legend('Prey','Predator')



실행결과입니다!


image