수치적 적분

이번시간에는 함수의 적분 값을 계산하기 위하여 근사 함수를 이용하는 방법에 대해 알아보겠습니다.

그 방법에는 선형 보간 다항식을 근사함수로 사용하는 사다리꼴 적분 방법과

이차 보간 다항식을 이용한 Simpson 적분방법이 있습니다.

사다리꼴 적분방법

먼저, 사다리꼴 적분방법에 대해 알아보겠습니다.

고등학교 때 배운 구분구적법과 유사하죠??

어려운 개념이 아니라고 생각합니다!

그럼 사다리꼴 적분방법을 사용하여 예제를 matlab으로 실행해보고, 얼마나 정확한지 확인해볼까요?

matlab 코드입니다!

clear; clc;
a=0; b=1; %적분 구간 끝 점
f=@(x)exp(x);
n=1000; 
h=(b-a)/n; %구간을 n등분 함
T=0; %적분값
for i=1:n
    T=T+f(a)+f(a+h); %밑변을 더함
    a=a+h;
end
T=T*h/2; %높이x1/2-> 사다리꼴 넓이
error=abs(exp(1)-1-T); %원래 값과의 오차
error

실행 결과입니다~!

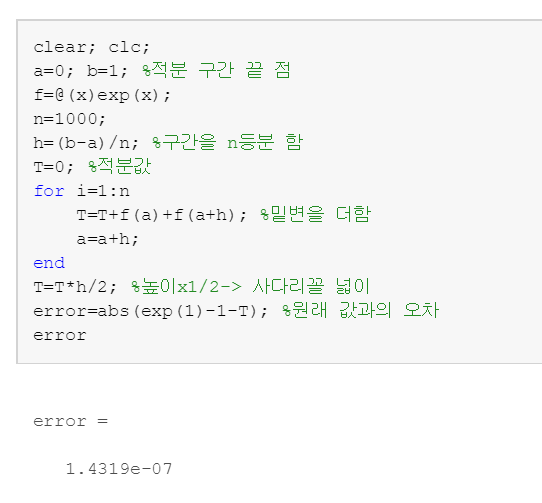
오차가 상당히 작은 것을 봐서 적분 값을 제대로 구하는 것을 볼 수 있습니다!

Simpson 방법

이번에는 사다리꼴 적분 방법보다 좀 더 정확한 방법에 대해 알아보겠습니다.

바로 Simpson 방법입니다!

Simpson 방법을 이용하여 아까 했던 예제에 대해 근사 값을 구해보겠습니다.

clear; clc;
a=0; b=1; %적분 구간 끝 점
f=@(x)exp(x);
n=1000; 
h=(b-a)/n; %구간을 n등분 함
T=0; %적분값
for i=1:n/2
    T=T+f(a)+4*f(a+h)+f(a+2*h); %Simpson 공식
    a=a+2*h;
end
T=T*h/3; 
error=abs(exp(1)-1-T); %원래 값과의 오차
error

실행결과입니다.

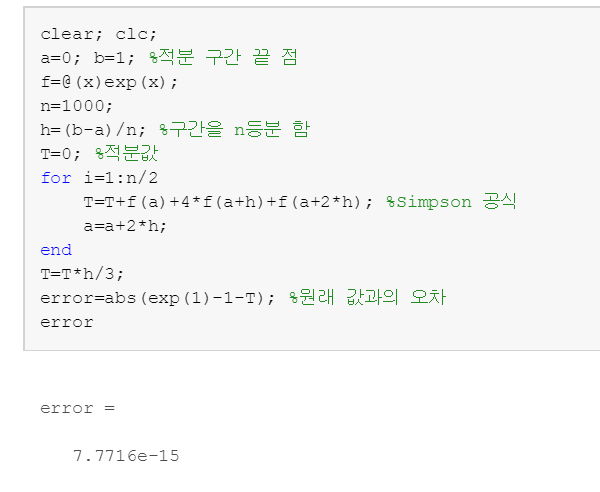
아까 사다리꼴 적분 방법을 사용할 때보다 오차가 훨씬 줄어든 것을 볼 수 있습니다!!

정말 대단하죠?? 다음 장에서는 특이적분에 대해 수치 적분 값을 구해보겠습니다~!