수치적미분

지금까지 저희는 어느 점의 미분계수를 구하기 위해 직접 도함수를 구해서 정의해야만 했습니다.

이번시간에는 도함수를 구하지 않고 미분 값을 수치적으로 구하는 방법에 대해 알아보겠습니다.

먼저, 전방차분법에 대해 알아보겠습니다~!

위의 식을 약간 수정하면 후방차분법이 됩니다!

좀 더 정확한 정확도를 갖는 방법에 대해 알아볼까요??

바로 중앙차분법입니다!

전,후방 차분법은 1차의 정확도를 가지고, 중앙차분법은 2차의 정확도를 가지므로,

중앙차분법이 좀 더 정확합니다~!

하지만 중앙차분법에도 단점이 존재합니다.

구간 [a,b]가 있다고 했을 때 왼쪽 끝 근방 x=a에서 중앙차분법을 사용할 수 없습니다.

이 때 사용할 수 있는 것이 3점 전방차분법입니다.

지금까지 수치적으로 미분 값을 구하는 방법에 대해 이론적으로 알아봤는데요~

한 번 matlab을 이용하여 제대로 구해지는지 확인해 볼까요??

중앙차분법을 사용하여 함수의 자코비안 행렬 값을 구해보겠습니다.

X=[0;2];
f1=@(X)X(1)^2+X(2)^2;
f2=@(X)2*X(1)^2+8*X(2);
F={f1,f2};
jacobian(F,X)

function J=jacobian(F,X)
    h=0.001; %적당히 작은 h
    n=length(X);
    m=length(F);
    J=zeros(m,n);

    for i=1:m
        for j=1:n
            V=zeros(n,1); % j번째 원소는 h, 나머진 0인 행렬을 만든다.
            V(j)=h;
            J(i,j)=(F{i}(X+V)-F{i}(X-V))/(2*h); %중앙차분법
        end
    end
end

실행결과를 봐볼까요??

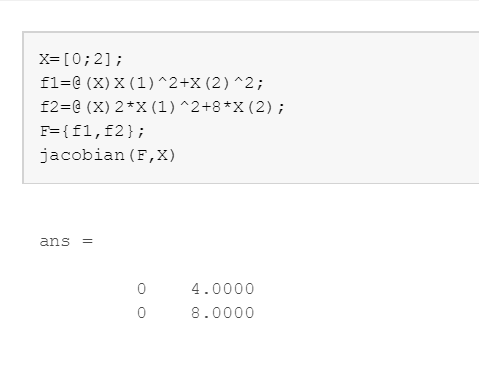
놀랍게도 결과 값이 일치하는 것을 볼 수 있습니다.

이제 저희는 미분 값을 구할 때 도함수를 구할 필요가 없습니다~ 정말 놀랍습니다.

다음시간에는 미분의 역연산인 적분 값을 수치적으로 구하는 방법에 대해 알아보겠습니다!