[matlab] 9.Steepest descent 방법

in Language on matlab


Steepest descent 방법



저번 시간에는 뉴턴 방법을 이용하여 비선형 방정식을 풀어봤습니다.

하지만 충분히 정확한 초기 근사값이 필요하다는 단점이 있는데요~~

이번 시간에는 정확하지 않은 초기 근사치에 대해서도 해에 비교적 잘 수렴시키는 Steepest descent 방법에 대해 알아보겠습니다.

일단 Steepest descent 방법에 대해 알아보기 전에, 미적분학에서 배웠던 gradient에 대해 먼저 알아보겠습니다.


image




image



steepest descent(gradient descent) 방법은 위의 gradient를 이용한 방법인데요~

이렇게 생각하시면 됩니다.

자신이 한치앞도 안보이는 산 속에 있을 때 산 정상으로 가기 위한 가장 쉬운 방법은

현재 위치에서 경사가 가장 높은 방향으로 오르는 것입니다.

가다보면 언젠가 산 정상에 도달하겠죠!

반대로 가장 깊은 골짜기를 찾고 싶다면 가장 가파른 내리막 방향으로 산을 내려가면 됩니다~

이와 같이 현재 위치에서 gradient 방향으로 이동해 가는 방법을 gradient ascent 방법,

극소점을 찾기 위해 gradient 반대 방향으로 이동해 가는 방법을 gradient descent 방법이라고 부릅니다.

더 자세히 알아보겠습니다.


image



그렇다면, gradient descent 방법으로 어떻게 연립방정식을 풀 수 있을까요??


image




image



한 번 matlab을 사용하여 다음 예제를 풀어보면서 이해를 해보겠습니다. 


예제

다음의 주어진 연립방정식을 Steepest descent 방법을 이용하여 x,y의

근사해를 구해보자. 초기 조건은 x0=0, y0=0으로 가정

3x-y=4, x+y=2



matlab에서 위의 Steepest descent 방법으로 해를 구하는 코드입니다. 


%%%%%%%%steep.m%%%%%%%%%%%
clc; clear;
f1=@(X)3*X(1)-X(2)-4;
f2=@(X)X(1)+X(2)-2; %함수부터 정의한다.
g=@(X)(f1(X))^2+(f2(X))^2; %g함수 정의
J=[3 -1;1 1]; %f1 f2의 자코비안 행렬 
g_del=@(X)2*J'*[f1(X);f2(X)]; %g함수의 gradient

x=[0 0]; %초기 값
tol=1.0e-7; %오차 
N=100; %최대 실행할 횟수
k=1; %실행한 횟수
alpha=1; %초기 알파 값

fprintf('count      resid      alpha      x       y \n');

while(k<=N)
    g1=g(x); %처음 x의 함수값
    z=g_del(x); %처음 x에서의 gradient 구함
    z0=sqrt(z(1)^2+z(2)^2); %gradient 크기
    if z0==0 %크기가 0이라면-> 극소(해)이므로 break
        break;
    end
    z=z/z0; %gradeint 크기를 1로 만든다.
    alpha1=0;
    alpha2=1;
    g2=g(x-alpha2*z'); %gradient 반대방향으로 처음 x값을 이동시켰을 때의 함수값
    
    %적절한 alpha를 찾는 과정
    while g2>=g1 %g1이 g2보다 커질 때 까지 alpha를 반으로 줄임(alpha가 너무 컸을 때 팅겨나감을 방지)
        alpha2=alpha2/2;
        g2=g(x-alpha2*z');
        if alpha2<tol/2 %alpha가 너무 작아지면 break
            break;
        end
    end
    g3=min(g1,g2); 
    if g3==g1 %alpha가 너무 작아졌을 때 alpha를 0으로 설정
        alpha=alpha1;
    else
        alpha=alpha2;
    end
    
    x=x-alpha*z'; %x이동
    gg=max(abs(g1),abs(g2)); 
    resid=abs(g3-gg); 
    
    fprintf(' %2d   %f   %f   %f   %f   \n',k,resid,alpha,x(1),x(2));
    
    if(resid<tol) %만약 감소하는 방향으로 이동했는데도 함숫값의 변화가 없다면,->극소
        break;
    end
    k=k+1;
end




실행결과입니다.


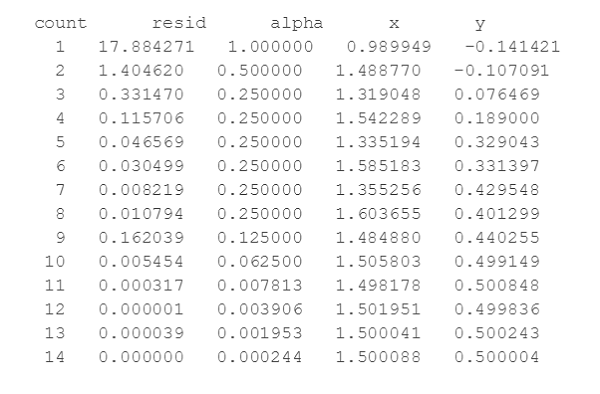
image



근사해 x,y가 잘 구해지는 것을 볼 수 있습니다.

이제 3개의 해를 가지는 연립방정식으로 확장해보겠습니다.

다음 예제를 보시죠!


image



위와 마찬가지로 matlab 코드를 적어보겠습니다!

먼저, 필요한 함수들을 정의하겠습니다. 


%%%%%%%f_func%%%%%%%
function F=f_func(x)
global f1 f2 f3; %함수가 전역적으로 선언했음을 알 수 있다.
F=[f1(x);f2(x);f3(x)];





%%%%%%%g_func%%%%%
function g=g_func(X)
    global f1 f2 f3; 
    g=f1(X)^2+f2(X)^2+f3(X)^2;
end





%%%%%%j_func%%%%%%%%
function J=j_func(x)
J= [2*x(1) -cos(x(2)) -0.5*sin(x(3));
    3 sin(x(2)) cos(x(3));
    2*x(1) 2*x(2) 2*x(3)];





%%%%%%%% steep2.m%%%%%%%%%%%%%%%
clc; clear;

%함수 정의 (global 전역변수로 정의)
global f1 f2 f3;
f1=@(X)X(1)^2-sin(X(2))+0.5*cos(X(3))-0.5;
f2=@(X)3*X(1)-cos(X(2))+sin(X(3));
f3=@(X)X(1)^2+X(2)^2+X(3)^2-0.95;

x=[0.5 0.5 0.5]; %초기 값
tol=1.0e-10; %오차
N=100; 
k=1;


fprintf('count      resid      alpha      x       y      z \n');

while k<=N
    g1=g_func(x); %초기 x에서의 함수값
    z=2*j_func(x)'*f_func(x); %초기 x에서의 gradient
    z0=sqrt(z(1)^2+z(2)^2+z(3)^2); %gradient의 크기
    if z0==0 %크기가 0이면 그 곳에서 극소
        break;
    end
    z=z/z0; %gradient 크기를 1로 함
    alpha1=0;
    alpha3=1;
    g3=g_func(x-alpha3*z'); % gradient 반대방향으로 x를 이동한 점에서의 함수 값
    
    %alpha를 잘 정하는 과정
    while g3>=g1
        alpha3=alpha3/2;
        g3=g_func(x-alpha3*z');
        if alpha3<tol/2
            break;
        end
    end
    alpha2=alpha3/2; %alpha1=0 과 alpha3의 사이 값을 이용
    g2=g_func(x-alpha2*z');
    g=min(g2,g3);
    if g==g2 %g2가 더 감소했다면 
        alpha=alpha2;
    else
        alpha=alpha3;
    end
    x=x-alpha*z'; %x 이동
    gg=max(abs(g1),abs(g2));
    resid=abs(g-gg);
    fprintf(' %2d   %f   %f   %f   %f   \n',k,resid,x(1),x(2),x(3));
    if resid<tol %더 이상 감소하지 않음 -> 극소
        break;
    end
    k=k+1;
end



다음은 실행결과입니다~


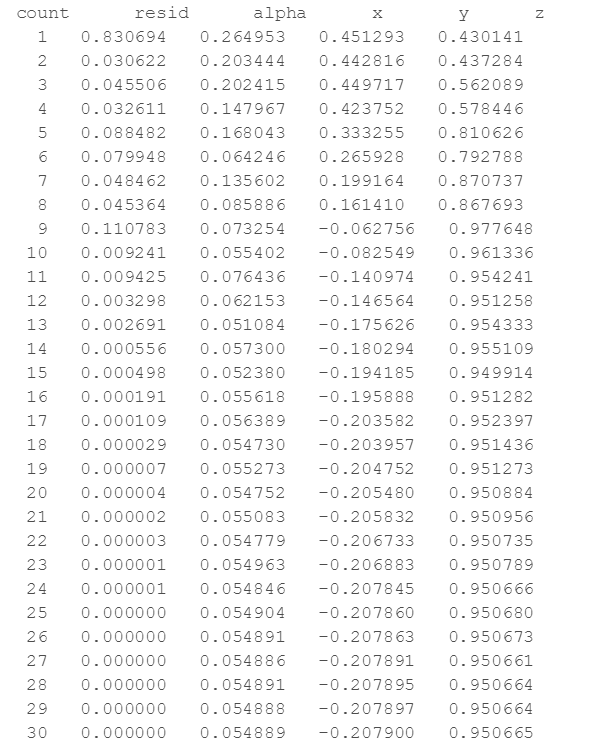
image



이렇게 이번 장까지 수치해를 구하는 방법에 대해 알아봤습니다.

사람의 손으로 구하기 힘든 해들을 컴퓨터는 정말 쉽게 구하네요~! 대단하죠?

놀라긴 아직 이릅니다. 다음 장부터는 수치적 미분에 대해 알아볼게요~!