[matlab] 8.비선형시스템의 수치해

in Language on matlab


비선형 시스템의 수치해



이번시간에는 다변수 함수로 이루어진 비선형 시스테의 해를 구하기 위해,

비선형 시스템을 선형화된 방정식들의 시스템으로 근사하여 해결하는 Newton 방법을 살펴보겠습니다.

먼저 이 절에서 사용할 몇 가지 다변수 비선형 시스템과 그 성질을 정의해 보겠습니다.


image




image




image




image



뉴턴 방법



이제 다변수 함수의 비선형 시스템을 뉴턴의 방법으로 풀어보겠습니다.


image



이해를 돕기 위해 역시 예제를 풀어보겠습니다~


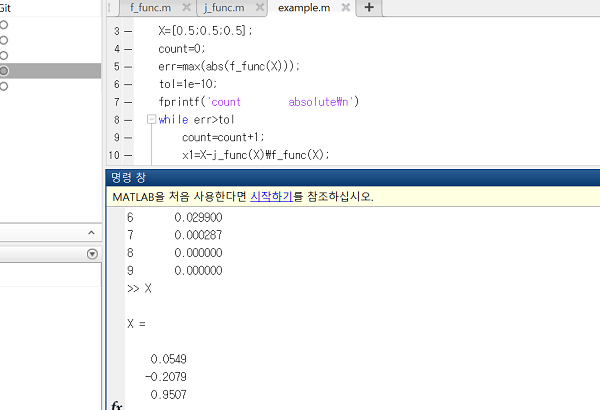
image



다음은 위의 예제를 뉴턴의 방법으로 푼 코드입니다. 


%%% F %%%
function F=f_func(X)
x=X(1); y=X(2); z=X(3);

f1=x^2-sin(y)+0.5*cos(z)-0.5;
f2=3*x-cos(y)+sin(z);
f3=x^2+y^2+z^2-0.95;

F=[f1;f2;f3];





%%% 자코비안

function J=j_func(X)
x=X(1); y=X(2); z=X(3);
J=[2*x -cos(y) -0.5*sin(z);3 sin(y) cos(z);2*x 2*y 2*z];





%%%%%뉴턴 방법
clear; clc;
X=[0.5;0.5;0.5];
count=0;
err=max(abs(f_func(X)));
tol=1e-10;
fprintf('count        absolute\n')
while err>tol
    count=count+1;
    x1=X-j_func(X)\f_func(X);
    X=x1;
    err=max(abs(f_func(X)));
    fprintf('%d       %f\n',count,err)
end



다음은 실행결과입니다. F(X)가 0에 수렴함을 알 수 있습니다. (X가 해)


image