[matlab] 7.방정식의수치해법

in Language on matlab


방정식의 수치해법



이번 시간에는 수치해석학의 하이라이트인 방정식의 근사해를 구하는 방법에 대하여 알아보겠습니다.

방정식의 수치해법에는 이분법, Newton 방법, Secant 방법 등이 있습니다~

여러 문제에 대하여 수학적으로 정확한 해를 정해(exact solution) 또는 참값이라고 부르고,

수치적 방법을 이용하여 구한 해를 수치해(numerical solution) 또는 근사값이라고 합니다.



이분법



이분법은 중간값 정리를 이용하여 해를 구하는 방법입니다~


image



이분법의 알고리즘은 다음과 같습니다.


image



역시 예시를 한 번 실행하면 이해가 빠르겠죠??


image



코드는 다음과 같습니다. 


a=0;
b=1;
n=0;
f='x^5-3*x-1';
tol=0.00001 %오차
c=(a+b)/2;
while b-c<tol
	n=n+1;
	x=b; fb=eval(f);
	x=c; fc=eval(f);
	if fb*fc<=0
		a=c; c=(a+b)/2;
	else
		b=c; c=(a+b)/2;
	end
end
c



실행 결과입니다~!


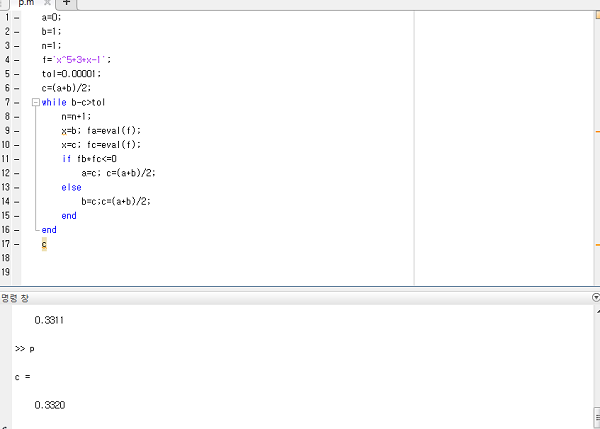
image



해가 잘 나오는 것을 볼 수 있습니다.

만약, 수치해의 값을 더 정밀하게 보고 싶으면 format long을 사용합니다.


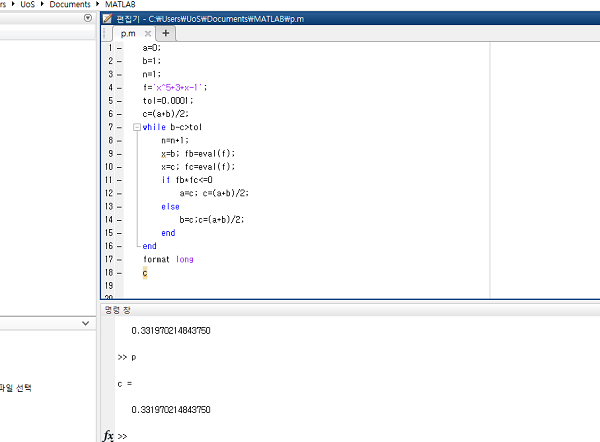
image



그리고 matlab도 c언어 처럼 fprintf로 출력이 가능합니다. 


fprintf('%2.0d %2.10f %2.4e \n',a,b,c)

%a를 정수로 출력, b를 소수점 열 째 자리까지 실수로 출력, c를 e를 이용한 실수로 출력



Newton 방법



Newton의 방법은 방정식 f(x)=0의 해를 구하는 수치해법 중에서

간편하고 신속하기 때문에 가장 잘 알려져있습니다.

뉴턴의 방법은 우선 연속인 도함수를 갖는 f(x)의 접선의 방정식을 이용하여 수치해를 구하는 방법입니다.


image



Newton 방법을 사용하여 아까 이분법에서 주어진 함수의 수치해를 구해보도록 하겠습니다. 


clear; clf; clc;
f='x^5+3*x-1';
df='5*x^4+3;
n=0; x0=0; %초기 값
tol=10^(-10); m=1;
fprintf('  n   x_n       f(x_n)       x_n-x(n-1) \n')
while m>=tol
	n=n+1; x=x0; y=eval(f); dy=eval(df);
	x1=x0-y/dy; m=abs(x1-x0);
	x=x1; y=eval(f);
	fprintf('%2.0f %2.4e %2.4e %2.4e \n,n,x1,y,x-x0)
	x0=x1;
end



실행 결과입니다.


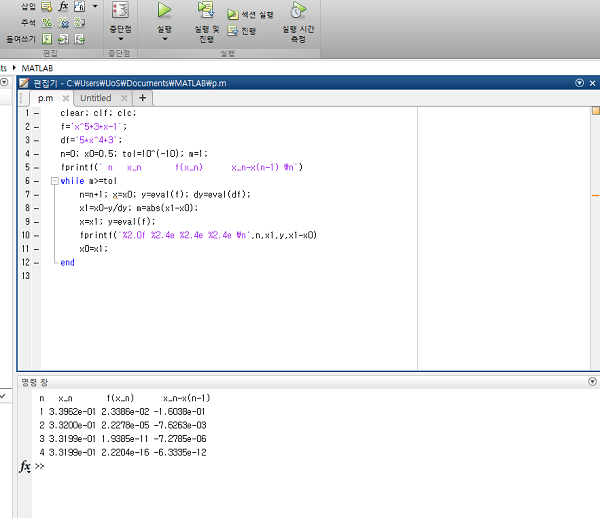
image



이분법을 사용할 때 보다 훨씬 빠르게 근사 값을 찾은 것을 볼 수 있습니다~!



Secant 방법



Newton 방법은 f(x)의 도함수를 이용하여 접선의 식을 구하고,

이 접선의 식이 x축과 만나는 점을 수치해로 구하는 방법이었습니다.

따라서 f(x)가 도함수를 갖지 않으면 Newton 방법을 사용할 수 없습니다.

이를 보정한 Secant 방법은 접선의 기울기 대신에 평균 변화율을 사용한 기법입니다.


image



아까 그 예제에 다시 secant 방법을 적용시켜보죠! 


clear; clf; clc;
f='x^5+3*x-1';
n=0; x0=0; x1=1; tol=10^(-10); m=1;
fprintf('  n   x_n       f(x_n)       x_n-x(n-1) \n')
while m>=tol
	n=n+1; x=x0; y0=eval(f); x=x1; y1=eval(f);
	m=abs(x1-x0);
	x2=x1-(y1*(x1-x0)/y1-y0));
	x=x2; y=eval(f);
	fprintf('%2.0f %2.4e %2.4e %2.4e \n',n,x,y,x1-x0)
	x0=x1;x1=x2;
end



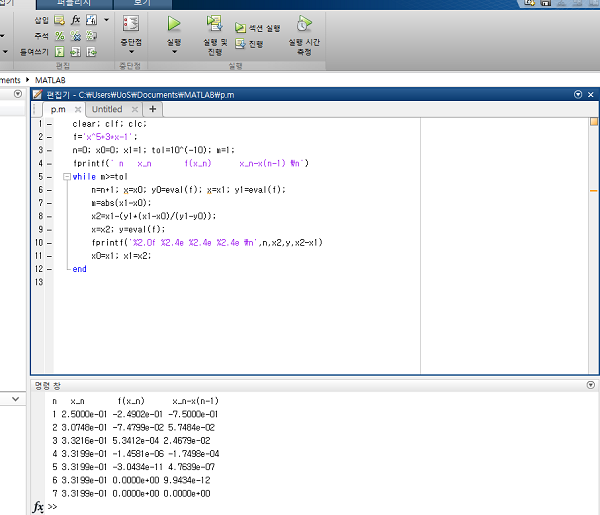
실행 결과입니다.(코드의 실수는 있을 수 있습니다.)


image



모든 해 구하기



이분법, Newton 방법, secant 방법으로 수치해를 구하는 법을 배워봤는데요..

위의 방법들은 어떤 하나의 해를 구하는 것이지, 모든 해를 구하는 방법은 아닙니다.

수치해석학에서 모든 해를 구하는 문제는 정말 어려운 문제입니다.

그러나 주어진 방정식의 해가 몇 개인지 미리 알고 있다면,

반복문을 써서 해가 모두 나올 때까지 위의 방법들을 사용하여

모든 해를 구할 수 있습니다.

예제를 통해 확인해보죠!


image



모든 해를 구하는 코드입니다. 


clear; clc; 
sol=[]; %해를 저장
numsol=0;
f=@(x)x^3-13*x^2+32*x-20; %f=inline('x^3->13*x^2+32*x+20','x')와 동일
df=@(x)3*x^2-26*x+32;
tol=10^(-6);
while numsol<3 %해가 모두 나올 때까지 반복
    x0=100*rand()-5; %초기값 임의로 지정
    m=1; 
    while m>=tol
        x=x0; y=f(x); dy=df(x);
        x1=x0-y/dy; m=abs(x1-x0);
        x0=x1;
    end
    flag=1;
    for i=1:numsol
        if abs(x1-sol(i))<tol %구한 해가 중복됬다면
            flag=0;
            break
        end
    end
    
    if flag
        if abs(df(x1))<tol %중근을 가진다면
            sol=[sol x1 x1];
            numsol=numsol+2;
        else
            sol=[sol x1];
            numsol=numsol+1;
        end
    end
end
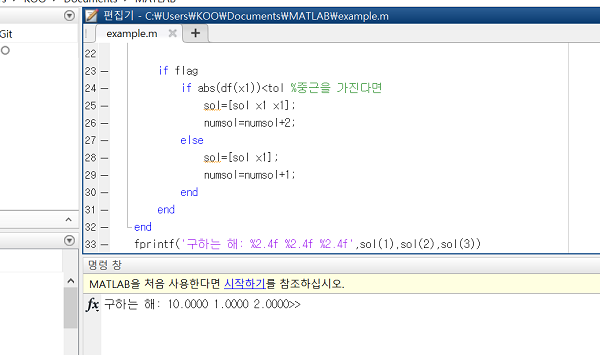
fprintf('구하는 해: %2.4f %2.4f >%2.4f',sol(1),sol(2),sol(3))



해를 잘 구하는 것을 볼 수 있습니다.


image