[matlab] 6.삼차스플라인 보간법
삼차 스플라인 보간법
불연속적인 n개의 점이 주어졌을 때
그 n개의 점을 지나는 n차 다항식을 구하는 방법을 보간법이라고 합니다.
저번 시간에는 보간법 중 가장 간단한 방법인 선형보간법에 대해 알아봤는데요~
주어진 점들을 직선으로 다 잇는 방법이었습니다.
하지만 직선으로 잇는 선형보간법을 사용하는 경우에는 원래 함수와 너무 나도 차이가 날 수 있고,
미분 불가능 한 점들도 너무 많이 생깁니다.
주어진 n개의 점을 지나는 둥글둥글한(매끄럽고 미분가능한) 함수를 구하고 싶은데요~
이 때 사용하는 방법이 바로 삼차 스플라인 보간법입니다!

쉽게 말해서 각 점들 사이 소구간을 삼차다항식으로 매꾸고 모든 구간을 합쳤을 때
미분가능하도록(심지어 도함수도 미분가능) 만드는 방법입니다.
한 번 하나의 예를 들어서 스플라인 함수를 직접 구해보며 이해를 돕도록 하겠습니다.
점 (0,1), (1,1), (2,5)에 대해 삼차 스플라인 함수를 구하시오


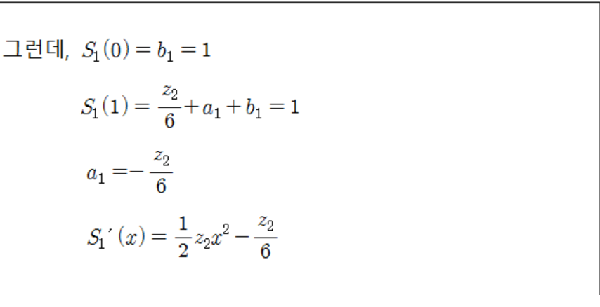

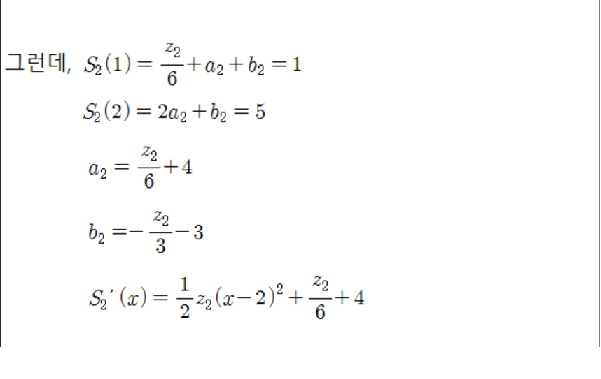

참 힘들게 구했습니다~!
그렇다면 삼차 스플라인 보간법을 이용하려면 계속 위의 과정처럼 복잡한 계산을 매번 해야할까요??
아닙니다! 다행히도 matlab의 내장함수에는
삼차 스플라인 보간법을 자동적으로 적용시켜주는 함수가 존재합니다.
바로, interp1이라는 함수입니다.
%interp1 예시
x=0:1:7;
y=sin(x);
xq=0:0.0001:7; %x를 잘게 쪼갠다
figure(1)
vq=interp1(x,y,xq,'spline'); % 점 x,y 를 지나는 스플라인 함수 구함
plot(x,y,'r.',xq,vq,'k-');
xlim([0 7]);
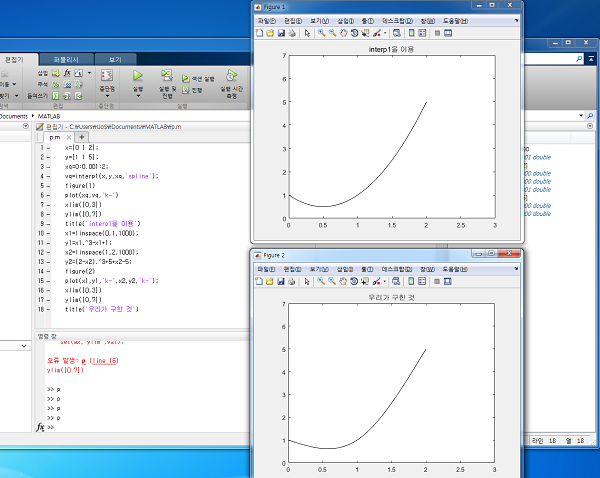
실행화면 입니다.
참고로 interp1에서 'spline' 대신에 'linear'를 넣으면 1차 보간법으로 구합니다.
'pchip'을 넣으면 shape-preserving 구분적 3차 보간을 합니다.
그렇다면 interp1으로 아까 우리가 구한 3차 스플라인 함수가 제대로 구해졌는지 확인해보죠!