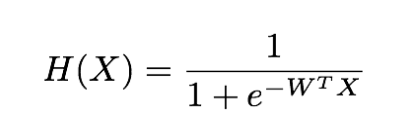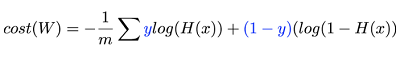Logistic(regression) classifier(1)

전 장의 예제에서는 어느 학생의 국어,영어,수학,과학 점수를 가지고서 대학의 합격여부를 예측하게끔 학습을 하였습니다.
하지만 예측 값을 0(불합격), 1(합격)으로 하고 싶었는데 그러지 못했었습니다.

이번시간에는 그 문제를 해결해 줄 classification(분류)를 배워 보겠습니다.

Logistic classifier도 4단계로 이뤄진다고 보면 됩니다.
1.training data를 준비한다.
2.Hypothesis(판별식)을 설정한다.
3.Cost함수를 설정한다.
4.cost함수를 최소화시키는 W,b를 구한다.

1.Training data set을 준비한다.

x_data(속성 값), y_data(결괏 값)을 따로 선언해줍니다.(실제 데이터)

# [학생1[국,영,수,과],학생2[국,영,수,과],학생3[국,영,수,과]]
x_data=[[100,92,95,72],[92,88,80,66],[70,59,68,77]]
y_data=[[1],[1],[0]]  #합격(1) 합격 불합격(0) 

2.Hypothesis(판별식)을 설정한다.

hypothesis는 데이터를 구분 짓는 직선이였죠~ 우리의 예측 값이기도 하구요.
하지만 이제는 hypothesis가 0과 1사이에 있게 하기 위해서 sigmoid라는 함수를 이용합니다.
(더이상 직선이라고 생각말고 구분시켜준다고만 생각)
sigmoid 함수는 다음과 같습니다.

원래의 hypothesis는 X*W+b인데 이 값의 범위는 무한합니다. 이를 sigmoid함수에 다시 넣으면 0과 1사이의 수로 값이 나오게 됩니다.

위의 공식은 b를 생략하였습니다.

그럼 새로운 hypothesis를 정의합니다~

hypothesis=tf.sigmoid(tf.matmul(X,W)+b)

tf.sigmoid는 sigmoid 함수에 대입 시켜준다.

3.Cost함수를 설정한다.

cost 함수는 우리가 hypothesis로 설정한 직선으로 구한 예측 값과 실제 값이 얼마나 다른가를 나타내는 함수이였습니다.

hypothesis가 더이상 직선이 아니기에 cost함수도 바뀌게 됩니다.
새로운 cost함수는 다음과 같습니다.

cost함수가 바뀌는 이유는 컴퓨터가 cost를 최소화시키기 좋게 하기 위한거다라고 생각하시면 됩니다.

새로운 cost함수를 정의 합니다.

cost=-tf.reduce_mean(Y*tf.log(hypothesis)+(1-Y)*tf.log(1-hypothesis))

4.cost함수를 최소화시키는 W,b를 구한다.

컴퓨터는 데이터를 훈련시키면서 cost 함수(우리가 예측한 값과 실제 값의 차이)를 작게 하는 W와 b 값을 구합니다.

이 부분은 역시 같습니다~!

optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.000001)
train=optimizer.minimize(cost)

다음 장에서 직접 tensorflow를 이용해서 직접 훈련도 시켜보고 예측 값도 구해보겠습니다.